Chapters
In this article, we will discuss how to solve the exponential functions that involve limits. But before discussing this, first, let us see what is an exponential function.
What is an Exponential Function?
An exponential function is a function in which the independent variable, i.e., x is the exponent or power of the base. It is of the form:
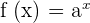
Here:
- a is a positive real number such that it is not equal to one
- The domain of the exponential function is all real numbers
- The range of the exponential function is all positive real numbers
- The y-intercept is (0, 1), and the horizontal asymptote is y is equal to zero
Standard Results of Limits
There are 5 standard results of limits which are discussed below. These standard results can be used as formulas while evaluating the limits of exponential functions.
Standard 1
\lim_{x \rightarrow a} \frac{x^n - a^n}{x - a} = n \cdot a ^ {n - 1}
Standard 2
\lim_{x \rightarrow 0} \frac{e^x - 1}{x } = 1
Standard 3
\lim_{x \rightarrow 0} \frac{a^x - 1}{x } = log_{e}a
Standard 4
\lim_{x \rightarrow 0} (1 + x) ^{\frac{1}{x}} = e
Standard 5
\lim_{x \rightarrow \infty} (1 + \frac{1}{x}) ^ x= e
In the next section, we will solve couple of examples in which we will be evaluating the limits of the exponential functions
Example 1
Evaluate the following exponential function:
\lim_{x \rightarrow 0} \frac {3 ^ {2x} - 7 ^ {4x}} {x}
Solution
It is given that the limit of the function should be evaluated as x approaches to 0. So, when we put 0 directly in the above expression, we get an indeterminate form of 
. Hence, here we will use L'Hospital's Rule which states that whenever we get an indeterminate form, we can take the derivative of the numerator and denominator separately and then apply the limit.
So, first, we will differentiate the numerator 
. The derivative of the first term is 
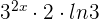. Similarly, the derivative of the second term 
is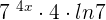 
.
Now, we will differentiate the denominator 
. The derivative of x is equal to 1. Substitute these derivatives in the above function like this:
=\lim_{x \rightarrow 0} \frac {3^{2x} \cdot 2 \cdot ln 3 - 7 ^{4x} \cdot 4 \cdot ln 7} {1}
Now, apply the limit on the above expression as shown below:
=\lim_{x \rightarrow 0} \frac {3^{0} \cdot 2 \cdot ln 3 - 7 ^{0} \cdot 4 \cdot ln 7} {1}
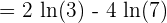
Example 2
Evaluate the following expression:
\lim_{x \rightarrow 0} \frac {5 ^ {2x} - 3 ^ {4x}} {5^{3x} - 2^{4x}}
Solution
It is given that the limit of the function should be evaluated as x approaches to 0. So, when we put 0 directly in the above expression, we get an indeterminate form of . Hence, here we will use L'Hospital's Rule which states that whenever we get an indeterminate form, we can take the derivative of the numerator and denominator separately and then apply the limit.
So, first, we will differentiate the numerator 5 ^ {2x} - 3 ^ {4x}. The derivative of the first term is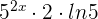 
. Similarly, the derivative of the second term 
is 
.
Now, we will differentiate the denominator 
. The derivative of the first term is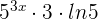 
. Similarly, the derivative of the second term 
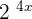is 
.
Substitute these derivatives in the above expression like this:
=\lim_{x \rightarrow 0} \frac {5^{2x} \cdot 2 \cdot ln 5 - 3 ^{4x} \cdot 4 \cdot ln 3 } {5^{3x} \cdot 3 \cdot ln 5 - 2 ^{4x} \cdot 4 \cdot ln 2}
Now, apply the limit on the above expression as shown below:
=\lim_{x \rightarrow 0} \frac {5^{0} \cdot 2 \cdot ln 5 - 3 ^{0} \cdot 4 \cdot ln 3 } {5^{0} \cdot 3 \cdot ln 5 - 2 ^{0} \cdot 4 \cdot ln 2}
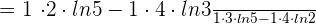
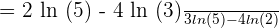
Example 3
Evaluate the limit of the following exponential function:
\lim_{x \rightarrow 0} \frac{e^x - e ^{-x}} {2x}
Solution
It is given that the limit of the function should be evaluated as x approaches to 0. So, when we put 0 directly in the above expression, we get an indeterminate form of . Hence, here we will use L'Hospital's Rule which states that whenever we get an indeterminate form, we can take the derivative of the numerator and denominator separately and then apply the limit.
First, we will find the derivative of the numerator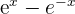 
which is equal to 
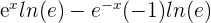. It is equal to 
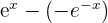. The derivative of the denominator is 2. We will substitute these values in the original function as shown below:
=\lim_{x \rightarrow 0} \frac{e^x + e^{-x}} {2}
Now, we will take the limit of the expression:
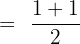
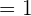
Example 4
Evaluate the limit of the following exponential function:
\lim_{x \rightarrow \infty} \frac{3^x + 2^x} {5}
Solution
It is easier to evaluate the above function because after substituting 
, we will not get the indeterminate form of or 
. So, there is no need to apply L'Hospital's Rule in this example.
\lim_{x \rightarrow \infty} \frac{3^{\infty} + 2^ {\infty}} {5}
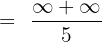
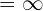
Example 5
Evaluate the following expression:
\lim_{x \rightarrow 2} \frac {5 ^ {x} + 7 ^ {3x}} {6x}
Solution
In this example, if we put x = 2 directly in the above expression, we do not get the indeterminate form, so L'Hospital's Rule is not applicable here. All we have to do is to substitute x = 2 in the above expression:
=\lim_{x \rightarrow 2} \frac {5 ^ {2} + 7 ^ {3 \cdot 2}} {6 (2)}
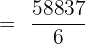
Example 6
Evaluate the following expression:
\lim_{x \rightarrow \infty} \frac {5e^ {4x} - e ^ {2x}} {6e^{4x} - 2^{-x} - e^ {2x}}
Solution
The primary concept that will be used in solving this problem will be the same as with the rational expressions. First, we will see the largest exponent in the numerator and the denominator, and then we will factor it out from both the numerator and the denominator. Since the limit in this example is plus infinity, hence we will only use the exponentials having positive exponents.
In this example, we will factor out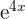 
from both the numerator and the denominator. Once we have done it, we will cancel out this common factor and take the limit of the remaining expression.
=\lim_{x \rightarrow \infty} \frac { e ^ {4x} (5 - e ^ {-2x})} {e ^ {4x} (6 - 2^{-5x} - e^ {-2x}}
Cancel out the common factor 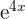from the numerator and the denominator like this:
= \lim_{x \rightarrow \infty} \frac { 5 - e ^ {-2x}} {6 - 2^{-5x} - e^ {-2x}}
Now, we will apply the limit as x approaches to infinity on the above remaining expression like this:
Did you like this article? Rate it!
Loading...
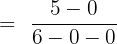
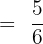
Derivative of denominator is wrong
Good catch—thanks for pointing that out! We’ll double-check the derivative in that section and make any necessary corrections. Really appreciate you taking the time to flag it. 👍
Thank you
Thank you Abbas! Good luck with your studies!
With regard to the Zero Over a Number item, is there a mis-statement? It’s immediately followed by “If a number is divided by zero which means that the numerator is zero and the denominator is the number, then the result is zero.”
Hi Mark,
You’re absolutely right to raise the question — there does appear to be a misstatement in that sentence. The phrase “If a number is divided by zero, which means that the numerator is zero and the denominator is the number…” is indeed misleading and should be corrected.
To clarify:
Zero divided by a number (e.g. 0 ÷ 5) equals 0.
A number divided by zero (e.g. 5 ÷ 0) is undefined.
We’ll update the sentence to reflect the correct mathematical explanation. We appreciate you catching that and helping us improve the accuracy of the content!
There is more than one size of infinity, though. What if you multiply the infinity of the whole numbers (Aleph-0) by the infinity of the real numbers (fraktur-c)?
Thanks a lot to you for this essentiol article.
Hi Piyash! Thanks for your comment, great to hear that you found this useful!
Very nice